Introduction
It’s quite common to think of physical space as \(\mathbb{R}^3\), but this perspective can be misleading, both from a mathematical and a physical standpoint. The main issue is that the structure of \(\mathbb{R}^3\) isn’t naturally invariant under displacements or other critical transformations, known as isometries, which are fundamental to Euclidean geometry. Instead, the three-dimensional space we encounter in Classical Physics (and even the four-dimensional spacetime in Special Relativity) is more accurately captured by the concept of affine spaces.
Affine spaces
To understand this better, let’s dive into what a real affine space is. A real affine space of finite dimension \(n\), denoted by \(\mathbb{A}^n\), is a collection of elements known as points, but with some additional structure:
- There’s an associated \(n\)-dimensional vector space \(V\), which we call the space of displacements or the space of free vectors.
- A mapping \(\mathbb{A}^n \times \mathbb{A}^n \ni (P, Q) \mapsto P - Q \in V\) that respects certain conditions:
- For every point \(Q\in \mathbb{A}^n\) and every vector \(\mathbf{v} \in V\), there’s a unique point \(P \in \mathbb{A}^n\) such that \(P - Q = \mathbf{v}\).
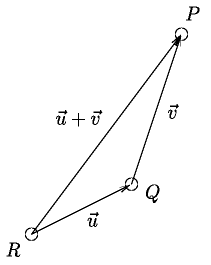
- For any three points \(P, Q, R \in \mathbb{A}^n\), the equation \(P - Q + Q - R = P - R\) always holds.
Additional definitions
Let’s define a few useful concepts:
- Given a point \(Q \in \mathbb{A}^n\) and a vector \(\mathbf{v} \in V\), the unique point \(P \in \mathbb{A}^n\) that satisfies \(P - Q = \mathbf{v}\) is denoted as \(Q + \mathbf{v}\).
- A line in \(\mathbb{A}^n\) originating from a point \(P\) with direction given by a vector \(\mathbf{v} \in V\) is described by the map \(\mathbb{R} \ni t \mapsto P + t\mathbf{v} \in \mathbb{A}^n\).
- A line segment is simply a restriction of the above map to a specific interval.
Properties
The following interesting properties hold for any points \(P, Q \in \mathbb{A}^n\) and vectors \(\mathbf{u}, \mathbf{v} \in V\):
- \(P - P = \mathbf{0}\).
- \((Q + \mathbf{u}) + \mathbf{v} = Q + (\mathbf{u} + \mathbf{v})\).
- \(P - Q = -(Q - P)\).
- \(P - Q = (P + \mathbf{u}) - (Q + \mathbf{u})\).
You can try proving these properties to deepen your understanding.
Coordinate systems on affine spaces
Now that we’ve established what an affine space is, let’s discuss how we can introduce coordinate systems on such spaces. A local coordinate system on an affine space \(\mathbb{A}^n\) is a map \(\psi: U \subset \mathbb{A}^n \rightarrow \mathbb{R}^n\) that satisfies:
- The map \(\psi\) is injective.
- The image \(\psi(U)\) is an open subset of \(\mathbb{R}^n\).
If \(U = \mathbb{A}^n\), we call the coordinate system global.
Cartesian coordinate systems
Every affine space has a family of global coordinate systems known as Cartesian coordinate systems. To define one, we need to:
- Choose a point \(O\) (the origin) and a basis \(\mathbf{e}_1, \ldots, \mathbf{e}_n\) for the vector space \(V\).
- Define a map \(f: \mathbb{A}^n \rightarrow \mathbb{R}^n\) by \(f(P) = \left((P - O)^1, \ldots, (P - O)^n\right)\).
Try proving that this map \(f\) is bijective, which will confirm that \(f\) is indeed a global coordinate system.
Non-Cartesian local coordinate systems, on the other hand, are referred to as curvilinear coordinate systems.
Properties of Cartesian coordinate systems
Suppose we have two Cartesian coordinate systems: \(\left(\mathbb{A}^n, f\right)\) with coordinates \(x^1, \cdots, x^n\), and another \(\left(\mathbb{A}^n, g\right)\) with coordinates \(x^{\prime 1}, \cdots, x^{\prime n}\), origin \(O^{\prime}\), and basis vectors \(\mathbf{e}_1^{\prime}, \ldots, \mathbf{e}_n^{\prime}\). If the relation between the basis vectors is:
\[ \mathbf{e}_i = \sum_j B^j{}_i \mathbf{e}_j^{\prime} \]
and \(O - O^{\prime} = \sum_i b^i \mathbf{e}_i\), then the following properties hold:
- The transformation map \(g \circ f^{-1}: \mathbb{R}^n \rightarrow \mathbb{R}^n\) is given by \(x^{\prime j} = \sum_{i=1}^n B^j{}_i\left(x^i + b^i\right)\).
- Conversely, the map \(f \circ g^{-1}: \mathbb{R}^n \rightarrow \mathbb{R}^n\) is expressed as \(x^i = -b^i + \sum_{j=1}^n\left(B^{-1}\right)^i{}_j x^{\prime j}\).
Again, try proving these transformations to see how coordinate systems relate to each other.
Affine transformations between affine spaces
Let’s now explore how we can map one affine space to another. A map \(\psi: \mathbb{A}_1^n \rightarrow \mathbb{A}_2^m\) between two affine spaces, with associated vector spaces \(V_1\) and \(V_2\), is called an affine transformation if:
- The map \(\psi\) is invariant under displacements, meaning that for any points \(P, Q \in \mathbb{A}_1^n\) and any vector \(\mathbf{u} \in V_1\), the equality \(\psi(P + \mathbf{u}) - \psi(Q + \mathbf{u}) = \psi(P) - \psi(Q)\) holds.
- The derivative map \(d\psi: V_1 \rightarrow V_2\), defined by \(d\psi(P - Q) = \psi(P) - \psi(Q)\), is a linear transformation between the vector spaces \(V_1\) and \(V_2\).
Proving that \(d\psi\) is well-defined and linear will help you understand the relationship between these spaces.
Isomorphism of affine spaces
An affine transformation \(\psi: \mathbb{A}_1^n \rightarrow \mathbb{A}_2^m\) is called an isomorphism if it is bijective. This concept is particularly important because it tells us when two affine spaces are structurally the same.
Properties of affine transformations
Affine transformations have several key properties:
- The inverse of an isomorphism is itself an affine transformation, making it an isomorphism as well.
- If \(\psi: \mathbb{A}_1^n \rightarrow \mathbb{A}_2^n\) is an isomorphism, then the derivative map \(d\psi: V_1 \rightarrow V_2\) is a vector space isomorphism.
- Affine transformations map straight lines to straight lines. Specifically, if \(P(t) := P + t \mathbf{u}\) describes a line in \(\mathbb{A}_1^n\), then \(\psi(P(t))\) defines a line in \(\mathbb{A}_2^m\).
- Given Cartesian coordinate systems on \(\mathbb{A}_1^n\) and \(\mathbb{A}_2^m\), the affine transformation \(\psi\) has a particularly simple form in these coordinates: \(x_2^i = c^i + \sum_{j=1}^n L^i{}_j x_1^j\), where the coefficients \(L^i{}_j\) and \(c^i\) depend on \(\psi\) and the chosen coordinate systems.
Proving these properties gives you a clearer view of how affine spaces relate to each other under transformations.
Group of displacements of affine spaces
In the context of affine spaces, the concept of displacements is crucial. For a given vector \(\mathbf{v} \in V\), we can define a mapping \(T_{\mathbf{v}}: \mathbb{A}^n \rightarrow \mathbb{A}^n\) that shifts every point \(P\) in the affine space by \(\mathbf{v}\). Formally, this map is defined as \(T_{\mathbf{v}}(P) = P + \mathbf{v}\). The collection of all such transformations, denoted \(\left\{T_{\mathbf{v}}\right\}_{\mathbf{v} \in V}\), forms what is known as the group of displacements of \(\mathbb{A}^n\). This group operates under the composition of mappings.
To explore this concept further, you can try proving that the set \(\left\{T_{\mathbf{v}}\right\}_{\mathbf{v} \in V}\) indeed forms a group under composition.
Properties
The group of displacements comes with several interesting properties:
- The group of displacements of \(\mathbb{A}^n\) is abelian, meaning that the order in which you apply displacements doesn’t matter; that is, \(T_{\mathbf{v}} \circ T_{\mathbf{u}} = T_{\mathbf{u}} \circ T_{\mathbf{v}}\) for any vectors \(\mathbf{u}, \mathbf{v} \in V\).
- The map \(V \ni \mathbf{v} \mapsto T_{\mathbf{v}}\) is injective, which means that each vector \(\mathbf{v}\) corresponds to a unique transformation. Moreover, this mapping is a group isomorphism when \(V\) is viewed as an abelian group under vector addition.
- Only the zero vector \(\mathbf{v} = \mathbf{0}\) satisfies \(T_{\mathbf{v}}(P) = P\) for some \(P \in \mathbb{A}^n\). In fact, this holds for every point \(P\), so the action of the group of displacements is free.
- For any two points \(P, Q \in \mathbb{A}^n\), there exists a displacement \(T_{\mathbf{v}}\) such that \(T_{\mathbf{v}}(P) = Q\). This property highlights the fact that the group of displacements acts transitively on the affine space.
These properties are foundational to understanding the structure of affine spaces. You might find it helpful to prove these properties yourself.
Group action
To generalize the idea of how a group can interact with a set, we use the concept of a group action. Let’s consider a set \(S\) and a group \(G\) with a neutral element \(e\) and a group operation \(\circ\). A group action is a map \(A: G \times S \ni (g, s) \mapsto A_g(s) \in S\), where \(A_g \in \mathcal{G}_S\) (the group of bijections on \(S\) under composition). For this map to be a valid group action, it must satisfy two key properties:
- The action of the neutral element is the identity: \(A_e = \text{id}\).
- The action respects the group operation: \(A_g \circ A_{g^{\prime}} = A_{g \circ g^{\prime}}\) for all \(g, g^{\prime} \in G\).
There are a few special types of group actions that are worth noting:
- The action is called free if \(A_g(s) = s\) for some \(s \in S\) implies \(g = e\).
- The action is transitive if for any two elements \(s, s^{\prime} \in S\), there exists a group element \(g \in G\) such that \(A_g(s) = s^{\prime}\).
- The action is faithful if the map \(G \ni g \mapsto A_g \in \mathcal{G}_S\) is injective, meaning that different elements of \(G\) induce different bijections on \(S\).
Whenever we have a group action, it naturally defines a group homomorphism from \(G\) to \(\mathcal{G}_S\). The image of this homomorphism, denoted \(G_S = \left\{A_g\right\}_{g \in G}\), is a subgroup of \(\mathcal{G}_S\). If the action is faithful, then this homomorphism is actually an isomorphism between \(G\) and \(G_S\).
To deepen your understanding, try proving the property that an action defines a group homomorphism and explore the implications of free, transitive, and faithful actions.